Hierarchische Strukturen mit Nested Sets

Hierarchische Strukturen mit Nested Sets in SQL zu implementieren, stellt den zweiten Beitrag einer dreiteiligen Kurzreihe dar, die sich mit hierarchischen Strukturen, deren Modellierung und SQL-Implementierung beschäftigt.

Im ersten Beitrag haben wir uns mit der Modellierung hierarchischer Strukturen mithilfe von Adjazenzlisten beschäftigt.

Hierarchische Strukturen mit Nested Sets

Die grundlegende Idee von Nested Sets ergibt sich aus deren Visualisierung, wenn wir quasi aus der Vogelperspektive auf eine Hierarchie herabblicken. Der Wurzel sind alle Datensätze einer Hierarchie direkt oder indirekt zugewiesen. Sie bildet folglich die größte Menge Alle der Wurzel zugeordneten Knoten bilden jeweils eine Teilmenge. Und so geht es weiter. Unser bereits bekanntes Beispiel einer Personalhierarchie, lässt sich dann wie folgt darstellen:

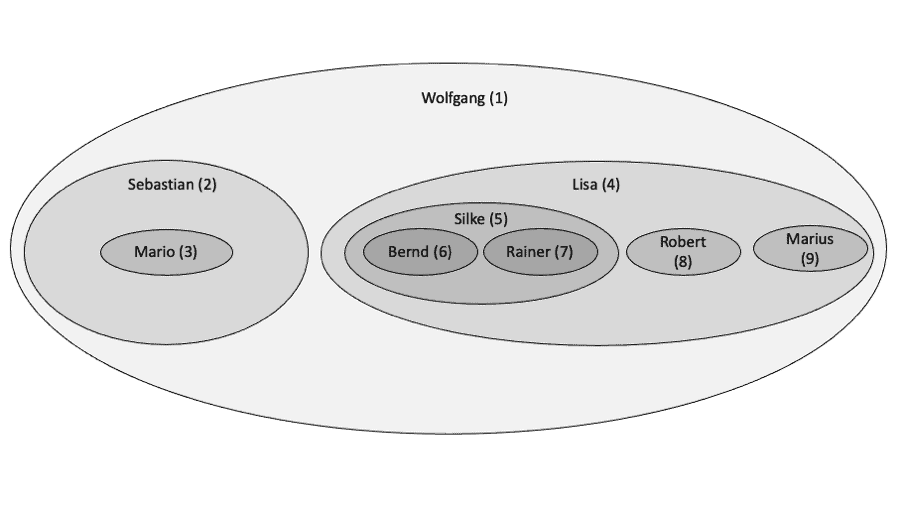
Regeln für Nested Sets

Zur Abbildung der Mengen und ihrer Beziehungen zueinander, werden Nummern vergeben. Jeder Knoten erhält einen Links- und einen Rechtswert. Dabei gilt: Der Links-Wert eines Knotens ist um 1 kleiner als der kleinste Links-Wert seiner untergeordneten Knoten, der Rechtswert ist um 1 größer als der größte Rechts-Wert seiner untergeordneten Knoten. Bei Blättern ist die Differenz zwischen Rechts- und Linkswert genau 1. Hieraus ergibt sich eine Nummerierung, der einzelnen Knoten, die in der folgenden Abbildung dargestellt ist.

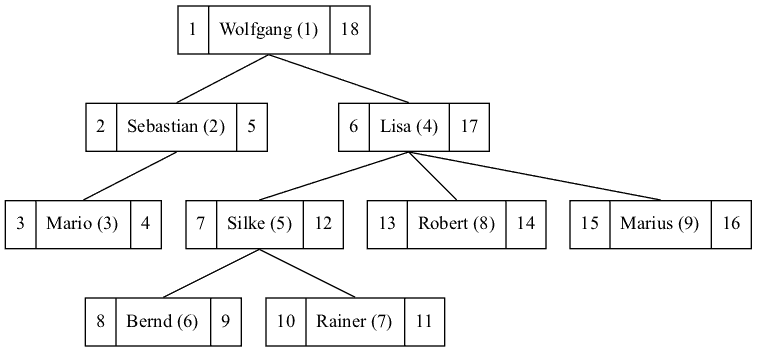
Aus der Abbildung ergeben sich einfache Regeln:

Die Wurzel eines Baumes hat den Links-Wert 1.
Bei einem Blatt beträgt die Differenz zwischen Rechts- und Links-Wert 1.
Einem Knoten untergeordnete Knoten haben Links-Werte, die größer sind als der Links- Wert des betrachteten Knotens. Die Rechts-Werte sind kleiner als der Rechts-Wert des betrachteten Knotens.
Die Vorgänger eines Knotens haben dementsprechend kleinere Links-Werte als der betrachtete Knoten und größere Rechts-Werte als derselbige.

Implizit wird durch die Reihenfolge des Einfügens eine Ordnung definiert. Weiter links im Baum stehende Knoten sind „älter“ als die Knoten der gleichen Ebene, die weiter rechts stehen. Semantisch macht eine solche Interpretation jedoch wenig Sinn.

Implementierung von Nested Sets

Die erforderliche Tabellenstruktur ist einfach. Statt Verweisen auf das Elternelement, werden je Datensatz zwei Felder verwendet, eines für den Links- und eines für den Rechts-Wert.

CREATE TABLE nested_set
(
    mnr   INT NOT NULL PRIMARY KEY REFERENCES personal (mnr)
                  ON UPDATE CASCADE,
    links INT NOT NULL,
    rchts INT NOT NULL
);
CREATE INDEX ON nested_set (rchts);
CREATE INDEX ON nested_set (links);

CREATE TABLE nested_set

(

mnr INT NOT NULL PRIMARY KEY REFERENCES personal (mnr)

ON UPDATE CASCADE,

links INT NOT NULL,

rchts INT NOT NULL

);

CREATE INDEX ON nested_set (rchts);

CREATE INDEX ON nested_set (links);

Hinweis: Die referenzierte Tabelle personal wurde in Teil 1 dieser Kurzreihe besprochen und vorgestellt.

Ganz offensichtlich kann die Ordnungsrelation, die die Subordination ausdrückt und die Struk- tur der Hierarchie definiert, nicht mit Hilfe von Fremdschlüsseln durchgesetzt werden. Die Wahrung der strukturellen Integrität ist also allein Aufgabe des Programmierers.

Allein das Einfügen eines Knotens darf dabei nicht unbedacht vorgenommen werden. Es muss stets eine Buchführung hinsichtlich der Knotennummerierung gegeführt werden. Wir betrachten diese und weitere Operationen im kommenden Abschnitt.

Operationen auf Nested Sets

Weil bei allen strukturellen Modifikationen eine Berechnung der Links- und Rechtswerte erforderlich ist, ist es notwendig, diese Operationen in gespeicherten Prozeduren zu kapseln. Nur so kann die strukturelle Konstistenz gewahrt und vor unbeabsichtigten Fehlern geschützt werden. Damit dies auch effektiv geschieht, dürfen Anwender keine INSERT-, UPDATE– oder DELETE-Operationen direkt auf der Tabelle der Organisationsstruktur durchführen. Es ist ein separater Anwender dafür anzulegen, der dann von den zu implementierenden Prozeduren genutzt wird, welche die Anwender für diese Operationen aufrufen. – Hier wird auf derartige Rechtevergabe verzichtet.

Knoten einfügen

Um einen Knoten einfügen zu können, muss zuerst der Elternknoten gefunden werden. Wird er nicht gefunden und ist die Anzahl der bereits eingefügten Knoten 0, so handelt es sich um den Wurzelknoten. Wird der Elternknoten nicht gefunden, obgleich bereits Knoten in der Hierarchie vorhanden sind, fehlt der Elternknoten und der neue Knoten kann nicht eingefügt werden.

CREATE PROCEDURE insert_knoten(mitarbeiter int, vorgesetzter int) AS $$
DECLARE r      INT := 0;
        anzahl INT := 0;
BEGIN
    SELECT rchts INTO r FROM nested_set WHERE mnr = vorgesetzter;
    SELECT COUNT(*) INTO anzahl FROM nested_set;
    IF r IS NULL AND anzahl = 0 THEN     -- Wurzelknoten einfügen
        r := 1;
    ELSEIF r IS NULL AND anzahl > 0 THEN -- Elternknoten fehlt
        RAISE EXCEPTION 'Elternknoten fehlt.';
    ELSE                                 -- normalen Knoten einfügen
        UPDATE nested_set
        SET rchts = rchts + 2
        WHERE rchts >= r;

        UPDATE nested_set
        SET links = links + 2
        WHERE links > r;
    END IF;
    INSERT INTO nested_set(mnr, links, rchts)
    VALUES (mitarbeiter, r, r+1);
    COMMIT;
END; $$ LANGUAGE plpgsql;

CREATE PROCEDURE insert_knoten(mitarbeiter int, vorgesetzter int) AS $$

DECLARE r INT := 0;

anzahl INT := 0;

BEGIN

SELECT rchts INTO r FROM nested_set WHERE mnr = vorgesetzter;

SELECT COUNT(*) INTO anzahl FROM nested_set;

IF r IS NULL AND anzahl = 0 THEN -- Wurzelknoten einfügen

r := 1;

ELSEIF r IS NULL AND anzahl > 0 THEN -- Elternknoten fehlt

RAISE EXCEPTION 'Elternknoten fehlt.';

ELSE -- normalen Knoten einfügen

UPDATE nested_set

SET rchts = rchts + 2

WHERE rchts >= r;

UPDATE nested_set

SET links = links + 2

WHERE links > r;

END IF;

INSERT INTO nested_set(mnr, links, rchts)

VALUES (mitarbeiter, r, r+1);

COMMIT;

END; $$ LANGUAGE plpgsql;

Wenn ein Knoten eingefügt werden kann, sind dessen Links- und Rechts-Werte zu ermitteln. Der Links-Wert ist der Rechts-Wert des Elternknotens, der Rechts-Wert ist um 1 größer. Alle Knoten, die hierarchisch rechts neben oder über dem Elternknoten stehen, müssen bezüglich ihrer Nummerierung geändert werden. Der Rechtswert ist um 2 zu erhöhen. Das gilt auch für den Elternknoten selbst. Es muss Platz im Nummerkreis geschaffen werden, den neuen Kindknoten einzufügen. Bei allen rechts vom Elternknoten stehenden Knoten ist ebenso der jeweilige Links-Wert um 2 zu erhöhen.

Jetzt können wir unsere Daten einfügen. Der erste Datensatz ist die Wurzel.

CALL insert_knoten(1, 1);
CALL insert_knoten(2, 1);
CALL insert_knoten(3, 2);
CALL insert_knoten(4, 1);
CALL insert_knoten(5, 4);
CALL insert_knoten(8, 4);
CALL insert_knoten(9, 4);
CALL insert_knoten(6, 5);
CALL insert_knoten(7, 5);

CALL insert_knoten(1, 1);

CALL insert_knoten(2, 1);

CALL insert_knoten(3, 2);

CALL insert_knoten(4, 1);

CALL insert_knoten(5, 4);

CALL insert_knoten(8, 4);

CALL insert_knoten(9, 4);

CALL insert_knoten(6, 5);

CALL insert_knoten(7, 5);

Abfragen der Hierarchie

Bevor wir uns weitere Operationen auf Nested Sets ansehen, wollen wir uns ansehen, wie wir eine so implementierte Hierarchie abfragen. Wir benötigen dies häufig bei der Implementierung der weiteren Operationen.

SELECT o1.mnr vnr, o2.mnr
FROM nested_set o1
JOIN nested_set o2 ON o2.links BETWEEN o1.links AND o1.rchts;

SELECT o1.mnr vnr, o2.mnr

FROM nested_set o1

JOIN nested_set o2 ON o2.links BETWEEN o1.links AND o1.rchts;

Die obige Abfrage gibt für jeden Vorgesetzten alle ihm zugeordneten Mitarbeiter, die ihm unterstellt sind, aus. Wir können dies ohne Rekursion bewirken. Ein einfacher Self-Join ist hinreichend. Zu einem gegebenen Mitarbeiter (o1.mnr) werden all die Mitarbeiter gesucht, deren Links-Wert innerhalb der Links-/Rechts-Werte des Vorgesetzten liegen. Die Rechts-Werte bedürfen keiner expliziten Betrachtung. Für Sie gilt selbiges, so dass die Betrachtung eines der beiden Werte hinreichend ist.

Entfernen von Knoten und das Schließen von Lücken

Bevor wir uns ansehen können, wie wir Knoten oder Teilbäume umhängen oder löschen, müssen wir uns Gedanken über die Buchführung im Nested Set machen. Im Gegensatz zur Adjazenzliste kann ein Knoten nicht einfach in der Hierarchie verschoben werden.

Löschen wir einen Knoten, so löschen wir (logischerweise) einen ganzen Teilbaum, wenn der zu löschende Knoten Kindknoten besitzt.

Hinweis: Man kann sich freilich auch überlegen, einen Knoten zu löschen, ohne gleich deren Kinder mit zu entfernen. M.E. ist es aber semantisch sinnvoller anzunehmen, die Kinder bei Bedarf erst zu verschieben und dann einen Knoten zu löschen. Wir einfach ein Knoten aus einem Nested Set gelöscht, kann die Hierarchie immer noch abgefragt werden, auch wenn der Nummernkreis Lücken aufweist. Die müssen vor Einfüge- oder Verschiebe-Operationen geschlossen werden.

Einen Knoten zu verschieben bedeutet, ihn am alten Platz zu löschen und ihn an einem neuen Platz wieder einzufügen. Besitzt der Knoten Kindknoten, verschieben wir einen Teilbaum. So oder so, entsteht beim Entfernen eine Lücke im Nummernkreis des momentan verbleibenden Baums. Dabei ist es egal, ob das Entfernen dauerhaft oder temporär ist, weil der Knoten an anderer Stelle wieder eingefügt, also verschoben werden soll. Die Lücke bewirkt vorerst keine Modifikation der strukturellen Logik des verbleibenden Baums, ist jedoch erst zu schließen, bevor der Knoten/Teilbaum wieder eingefügt werden kann.

Beginnen wir, um das Unterfangen übersichtlich zu halten, mit dem Entfernen eines Knotens sowie dem Schließen einer Lücke, die entsteht, wenn ein Blatt oder Teilbaum gelöscht wird.

Löschen eines Knotens oder Teilbaums

Wenn ein Knoten Kindknoten besitzt, ist das Löschen eines Knotens identisch zum Löschen eines Teilbaums. Die folgende Routine entfernt daher den angegebenen Knoten sowie eventuell davon abhängige Unterknoten.

CREATE PROCEDURE delete_knoten(IN mitarbeiter int) AS $$
BEGIN
    DELETE
    FROM nested_set
    WHERE links BETWEEN (
        SELECT links
        FROM ( SELECT * FROM nested_set ) hlp
        WHERE mnr = mitarbeiter)
         AND ( SELECT rchts
               FROM (  SELECT * FROM nested_set ) hlp
               WHERE mnr = mitarbeiter );
    CALL korrigiere_nummernkreis();
END; $$ LANGUAGE plpgsql;

CREATE PROCEDURE delete_knoten(IN mitarbeiter int) AS $$

BEGIN

DELETE

FROM nested_set

WHERE links BETWEEN (

SELECT links

FROM ( SELECT * FROM nested_set ) hlp

WHERE mnr = mitarbeiter)

AND ( SELECT rchts

FROM ( SELECT * FROM nested_set ) hlp

WHERE mnr = mitarbeiter );

CALL korrigiere_nummernkreis();

END; $$ LANGUAGE plpgsql;

Das Traversieren des (Unter-)Baumes entspricht Listing Listing 5. Weil es bei DELETE jedoch nicht zulässig ist, die Tabelle, aus welcher zu löschen ist, mit sich selbst zu verknüpfen, verwenden wir entsprechende Unterabfragen.

Nach dem Entfernen der Knoten weist der verbliebene Baum eine mehr oder minder große Lücke in dessen Knoten-Nummerierung auf. Diese ist zu schließen.

Schließen einer Lücke

Das Schließen einer Lücke geschieht in zwei Schritten. Zuerst ermitteln wir den noch aktuellen Nummernkreis des gerade modifizierten Baums. Hierzu implementieren wir eine Sicht. Sie sammelt alle verbliebenen Nummern. Diese bilden die Basis für die im nächsten Schritt durchzuführende Re-Nummerierung.

CREATE OR REPLACE VIEW nummernkreis (nr)
AS
SELECT * FROM (  SELECT links
                 FROM nested_set
                 WHERE links > 0
                 UNION ALL SELECT rchts
                 FROM nested_set
                 WHERE rchts > 0) nummern
ORDER BY 1;

CREATE OR REPLACE VIEW nummernkreis (nr)

SELECT * FROM ( SELECT links

FROM nested_set

WHERE links > 0

UNION ALL SELECT rchts

FROM nested_set

WHERE rchts > 0) nummern

ORDER BY 1;

Die WHERE-Bedingungen wurden im „vorauseilenden Gehorsam“ implementiert. Wir werden zu verschiebende Knoten negieren, deren Nummerierung mit einem Minuszeichen versehen, um sie als zu verschiebende Knoten zu kennzeichnen.

Für die Re-Nummerieung nutzen wir aus, dass der Baum, trotz der Lücke im Nummernkreis immer noch ein strukturell valider Baum ist und die Nummerierung der Knoten fortlaufend, wenn auch mit Unterbrechungen, ist. Das UPDATE betrifft alle Knoten im Baum. Durch einfaches Zählen wird die jeweils einzutragende Nummer ermittelt.

CREATE PROCEDURE korrigiere_nummernkreis() AS $$
BEGIN
    UPDATE nested_set
    SET links = (SELECT COUNT(*) FROM nummernkreis WHERE nr <= links),
        rchts = (SELECT COUNT(*) FROM nummernkreis WHERE nr <= rchts) WHERE links > 0; -- zu verschiebende Unterbäume sind negiert
END; $$ LANGUAGE plpgsql;

CREATE PROCEDURE korrigiere_nummernkreis() AS $$

BEGIN

UPDATE nested_set

SET links = (SELECT COUNT(*) FROM nummernkreis WHERE nr <= links),

rchts = (SELECT COUNT(*) FROM nummernkreis WHERE nr <= rchts) WHERE links > 0; -- zu verschiebende Unterbäume sind negiert

END; $$ LANGUAGE plpgsql;

Bei der Re-Nummerierung ist es, was die negierten Knoten angeht, ausreichend, sich an einem der Nummerierungswerte zu orientieren. Knoten mit negativen Nummerierungswerten werden von der Re-Numerierung ausgeschlossen. Die Nummerierung des momentan verbliebenden Baums, wenn ein Knoten oder Teilbaum entfernt wurde, ist nach Ausführung der Prozedur korrigiere_nummernkreis() wieder durchgängig.

Verschieben eines Knotens oder Teilbaums

Um einen Knoten oder Teilbaum, wenn der zu verschiebende Knoten Kindknoten besitzt, zu verschieben, ist er zuerst aus dem Baum herauszulösen.

Vielfach werden hierzu Algorithmen präsentiert, die den Teilbaum in eine temporäre Tabelle kopieren, ihn dann in der Hierarchie löschen, die entstehende Lücke schließen und danach an der angestrebten Stelle (aus der temporären Tabelle heraus) wieder einfügen.

Das Umkopieren ist jedoch nicht erforderlich. Es ist lediglich dafür zu sorgen, den zu verschiebenden Knoten/Teilbaum kenntlich zu machen. Weil alle Links-/Rechts-Werte positiv sind, reicht deren Negation. So ist klar, dass die so markierten Knoten vorerst aus dem Baum isoliert sind. Das Umkopieren kann erspart werden.

CREATE PROCEDURE move_knoten(
    IN mitarbeiter int, IN vorgesetzter INT)  AS $$
    DECLARE schrittweite int;
    DECLARE l_m int;  -- Links-Wert des zu verschiebenden Knotens
    DECLARE r_m int;  -- Rechts-Wert des zu verschiebenden Knotens
    DECLARE r_v int;  -- Rechts-Wert des neuen Elternknotens
BEGIN

    /* Wurzel des zu verschiebenden Knotens/Teilbaums */
    SELECT links, rchts INTO l_m, r_m FROM nested_set
    WHERE mnr = mitarbeiter;

    /* zu verschiebenden Teilbaum negieren
       ----------------------------------- */
    UPDATE nested_set ns
        SET links = -links,
            rchts = -rchts
    FROM (
            SELECT o1.mnr vnr, o2.mnr mnr
            FROM nested_set o1
            JOIN nested_set o2 ON o2.links BETWEEN o1.links AND o1.rchts
            WHERE o1.mnr = mitarbeiter
         ) hlp
    WHERE ns.mnr = hlp.mnr;

    /* Nummernkreis des verbleibenden Baumes reparieren
       ------------------------------------------------ */
    CALL korrigiere_nummernkreis();

    /* Evtl. neuen Rechts-Wert des neuen Vorgesetztenknoten ermitteln */
    SELECT rchts INTO r_v FROM nested_set WHERE mnr = vorgesetzter;

    /* Platz im verbliebenen Baum schaffen
       ----------------------------------- */
    schrittweite := (r_m - l_m + 1); -- Platzbedarf

    UPDATE nested_set -- rechte Nummern ändern
    SET rchts = rchts + schrittweite
    WHERE rchts >= r_v;

    UPDATE nested_set -- linke Nummern ändern
    SET links = links + schrittweite
    WHERE links > r_v;

    /* herausgelösten Subtree durch Re-Nummerierung einfügen
       ----------------------------------------------------- */

    /* Schrittweite der Nummernänderung berechnen */
    schrittweite := r_v + schrittweite - r_m - 1;

    /* Teilbaum korrigieren und einhängen */
    UPDATE nested_set
    SET rchts = -rchts + schrittweite
    WHERE rchts < 0;
    UPDATE nested_set
    SET links = -links + schrittweite
    WHERE links < 0;
    COMMIT;
END; $$ LANGUAGE plpgsql;

CREATE PROCEDURE move_knoten(

IN mitarbeiter int, IN vorgesetzter INT) AS $$

DECLARE schrittweite int;

DECLARE l_m int; -- Links-Wert des zu verschiebenden Knotens

DECLARE r_m int; -- Rechts-Wert des zu verschiebenden Knotens

DECLARE r_v int; -- Rechts-Wert des neuen Elternknotens

BEGIN

/* Wurzel des zu verschiebenden Knotens/Teilbaums */

SELECT links, rchts INTO l_m, r_m FROM nested_set

WHERE mnr = mitarbeiter;

/* zu verschiebenden Teilbaum negieren

----------------------------------- */

UPDATE nested_set ns

SET links = -links,

rchts = -rchts

FROM (

SELECT o1.mnr vnr, o2.mnr mnr

FROM nested_set o1

JOIN nested_set o2 ON o2.links BETWEEN o1.links AND o1.rchts

WHERE o1.mnr = mitarbeiter

) hlp

WHERE ns.mnr = hlp.mnr;

/* Nummernkreis des verbleibenden Baumes reparieren

------------------------------------------------ */

CALL korrigiere_nummernkreis();

/* Evtl. neuen Rechts-Wert des neuen Vorgesetztenknoten ermitteln */

SELECT rchts INTO r_v FROM nested_set WHERE mnr = vorgesetzter;

/* Platz im verbliebenen Baum schaffen

----------------------------------- */

schrittweite := (r_m - l_m + 1); -- Platzbedarf

UPDATE nested_set -- rechte Nummern ändern

SET rchts = rchts + schrittweite

WHERE rchts >= r_v;

UPDATE nested_set -- linke Nummern ändern

SET links = links + schrittweite

WHERE links > r_v;

/* herausgelösten Subtree durch Re-Nummerierung einfügen

----------------------------------------------------- */

/* Schrittweite der Nummernänderung berechnen */

schrittweite := r_v + schrittweite - r_m - 1;

/* Teilbaum korrigieren und einhängen */

UPDATE nested_set

SET rchts = -rchts + schrittweite

WHERE rchts < 0;

UPDATE nested_set

SET links = -links + schrittweite

WHERE links < 0;

COMMIT;

END; $$ LANGUAGE plpgsql;

Ausgesuchte Abfragen auf Teilbäumen eines Nested Sets

Die Ebenen einer Hierarchie bestimmen wir durch Zählen. Weil BETWEEN auch gleiche Werte mitzählt (also auch den Knoten selbst), müssen wir von COUNT(*) eins abziehen.

SELECT n.mnr, count(*) - 1 AS ebene
FROM nested_set AS n,
     nested_set AS p
WHERE n.links BETWEEN p.links AND p.rchts
GROUP BY n.mnr
ORDER BY ebene, n.links;

SELECT n.mnr, count(*) - 1 AS ebene

FROM nested_set AS n,

nested_set AS p

WHERE n.links BETWEEN p.links AND p.rchts

GROUP BY n.mnr

ORDER BY ebene, n.links;

Um den Pfad von der Wurzel zu einem bestimmten Knoten, hier Knoten 8, auszugeben, können wir folgendes Statement verwenden:

SELECT p.*
FROM nested_set n,
     nested_set p
WHERE n.links BETWEEN p.links AND p.rchts
  AND n.mnr = 8
ORDER BY n.links;

SELECT p.*

FROM nested_set n,

nested_set p

WHERE n.links BETWEEN p.links AND p.rchts

AND n.mnr = 8

ORDER BY n.links;

Den kompletten Teilbaum unterhalb eines bestimmten Knotens bestimmen wir so:

SELECT o.mnr,
       count(p.mnr) - 1 AS ebene
FROM nested_set AS n,
     nested_set AS p,
     nested_set AS o
WHERE o.links BETWEEN p.links AND p.rchts
  AND o.links BETWEEN n.links AND n.rchts
  AND n.mnr = 4
GROUP BY o.mnr
ORDER BY o.links;

SELECT o.mnr,

count(p.mnr) - 1 AS ebene

FROM nested_set AS n,

nested_set AS p,

nested_set AS o

WHERE o.links BETWEEN p.links AND p.rchts

AND o.links BETWEEN n.links AND n.rchts

AND n.mnr = 4

GROUP BY o.mnr

ORDER BY o.links;

Last but not least wollen wir zu jedem Knoten die Anzahl seiner Nachfolger bestimmen:

SELECT n.mnr,
       count(*) - 1                       AS ebene,
       round((n.rchts - n.links - 1) / 2) AS nachfolger
FROM nested_set AS n,
     nested_set AS p
WHERE n.links BETWEEN p.links AND p.rchts
GROUP BY n.mnr
ORDER BY ebene, n.links;

SELECT n.mnr,

count(*) - 1 AS ebene,

round((n.rchts - n.links - 1) / 2) AS nachfolger

FROM nested_set AS n,

nested_set AS p

WHERE n.links BETWEEN p.links AND p.rchts

GROUP BY n.mnr

ORDER BY ebene, n.links;

Wir könnten jetzt noch weitere Abfragen durchspielen. Das entscheidende, was man im Zusammenhang von hierarchischen Strukturen mit Nested Sets begreifen muss, ist die Systematik, die sich aus der Links-Rechts-Nummerierung der Knoten ergibt. Sie bestimmt die Logik, wie die auszuführenden Operationen auszusehen haben, um ein korrektes Resultat zu liefern.

Zwischenfazit

Während Adjazenzlisten Rekursion voraussetzen, lassen sich hierarchische Strukturen mit Nested Sets mit jedem Datenbankmanagementsystem implementieren. Die strukturelle Integrität der Struktur ist jedoch relativ aufwendig mithilfe prozeduralen Codes zu gewährleisten, weil sämtliche Änderungen vergleichsweise komplex und aufwändig sind. Es obliegt ganz und gar dem Programmierer, diese Operationen korrekt zu definieren. Es sollte daher vermieden werden, die Tabelle mit dem Nested Set direkt dem Anwender zugänglich zu machen. Ein geeignetes Berechtigungskonzept kann umkoordinierte Zugriffe wirksam verhindern.

Hierarchische Strukturen mit Nested Sets zu modellieren ist daher vor allem dann ein Mittel der Wahl, wenn das gewählte Datenbankmanagementsystem keine Rekursen zur Verfügung stellt und/oder es auf die Ausführungsgeschwindigkeit der Abfragen ankommt. Der Preis sind aufwändige Änderungsoperationen. Nested Sets sind daher wenig geeignet, wenn Hierarchien mit vielen Tausend Knoten gespeichert werden sollen, deren Positionen im Baum häufigen Änderungen unterworfen sind.

Teil 1: Hierarchische Strukturen mit Adjazenzlisten

Teil 3: Hierarchische Strukturen mit Closure Tables

Karsten Brodmann

Karsten Brodmann hat an der Universität Osnabrück BWL/Wirtschaftsinformatik studiert. Er hat viele Jahre in der IT gearbeitet und dort Web- und Datenbankanwendungen entwickelt. Seit Gründung der Punkt-Akademie veröffentlicht Karsten Brodmann auch Schulungsvideos zur Datenbankentwicklung, Unix und Programmierung bei Udemy. In seiner Freizeit fotografiert Karsten Brodmann gerne. Seit vielen Jahren fotografiert er analog und digital. Dabei behält er jeweils den gesamten Workflow in der eigenen Hand, von der Aufnahme über die Dunkelkammer oder auch den Scanner sowie die Bildbearbeitung und den Ausdruck am PC.

Punkt-Akademie

Wissen auf den Punkt gebracht

Hierarchische Strukturen mit Nested Sets

Hierarchische Strukturen mit Nested Sets

Regeln für Nested Sets

Implementierung von Nested Sets

Operationen auf Nested Sets

Knoten einfügen

Abfragen der Hierarchie

Entfernen von Knoten und das Schließen von Lücken

Löschen eines Knotens oder Teilbaums

Schließen einer Lücke

Verschieben eines Knotens oder Teilbaums

Ausgesuchte Abfragen auf Teilbäumen eines Nested Sets

Zwischenfazit

Karsten Brodmann

Schreibe einen Kommentar Antworten abbrechen