Hierarchische Strukturen mit Adjazenzlisten in SQL zu implementieren, stellt den ersten Beitrag einer dreiteiligen Kurzreihe dar, die sich mit hierarchischen Strukturen, deren Modellierung und SQL-Implementierung beschäftigt.
Bäume und Hierarchien mit SQL zu modellieren und zu handhaben, geben immer wieder Anlass zu Fragen. Das spiegeln jedenfalls die einschlägigen Foren im Internet wider. In der Tat war die mangelnde Unterstützung hierarchischer Strukturen der Grund, weshalb viele den relationalen Datenbankmanagementsystemen nur wenige Erfolgschancen eingeräumt haben, als E.F. Codd ehedem das relationale Datenbankkonzept vorstellte.
Hierarchische Strukturen mit Adjazenzlisten
In einem Artikel beschrieb E.F. Codd beispielhaft eine Methode, die Implementierung hierarchischer Strukturen mithilfe von Adjazenzlisten und SQL umzusetzen. Sein Beispiel bestand darin, die Beziehungen zwischen den Namen von Mitarbeitern und deren Vorgesetzten in Form einer Adazenzliste abzubilden.
Oracle war dann das erste kommerzielle Datenbankmanagementsystem, welches auf dem relationalen Datenbankkonzept basierte und SQL verwendete. In der Beispieldatenbank, die dem Produkt beigefügt war, wurde das Beispiel von E.F. Codd in der „Scott/Tiger“-Datenbank aufgegriffen. Es nutze ebenfalls eine Adjazenzliste, um eine Personalhierarchie in einer einzigen Tabelle zu modellieren. Dieses Beispiel hat Schule gemacht. Wir finden analoge Implementierungen in vielfältigen Beiträgen, die hierarchische Strukturen mithilfe von SQL behandeln.
Einfaches Adjazenzlistenmodell
Das folgende Datenmodell greift das Oracle-Beispiel auf. Diese Datenstruktur findet man auch in vielfältigen Beiträgen, die sich mit der Abbildung hierarchischer Datenstrukturen in relationalen Datenbankmanagementsystemen befassen.
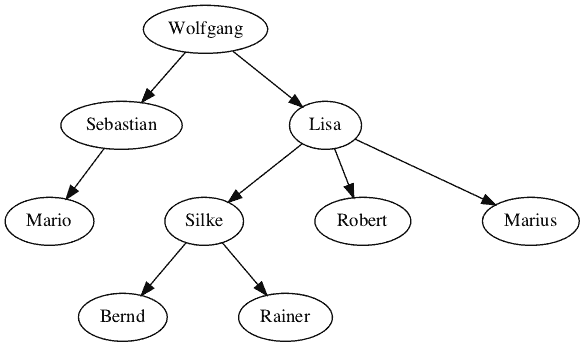
Die Idee ist einfach. Ein Mitarbeiter wird mit seinem direkten Vorgesetzten in Beziehung gesetzt. Der oberste Chef hat keinen Vorgesetzten. Das entsprechende Attribut wird daher auf NULL gesetzt.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
CREATE TABLE personalorganisation -- Version 1 ( mitarbeiter VARCHAR(20) NOT NULL PRIMARY KEY, vorgesetzter VARCHAR(20), -- NULL kennzeichnet die Wurzel geburtsdatum DATE NOT NULL -- weitere Attribute ); INSERT INTO personalorganisation(mitarbeiter, vorgesetzter, geburtsdatum) VALUES ('Wolfgang', NULL, '1980-12-06') , ('Sebastian', 'Wolfgang', '1979-10-03') , ('Mario', 'Sebastian', '2002-09-03') , ('Lisa', 'Wolfgang', '1980-12-01') , ('Silke', 'Lisa', '1985-01-06') , ('Bernd', 'Silke', '1989-11-27') , ('Rainer', 'Silke', '1995-12-01') , ('Robert', 'Lisa', '1984-07-16') , ('Marius', 'Lisa', '1989-02-05'); |
Personennamen als Schlüssel zu verwenden, ist keine gute Programmierpraxis. Um die Diskussion einfach zu halten und auf das Wesentliche zu konzentrieren, ignorieren wir diesen Fakt vorerst. Das gewählte Modell ist nicht nur nicht normalisiert, es definiert auch keinerlei Regeln, welche die hierarchische Struktur gewährleisten, die abgebildet werden soll. Es stellt lediglich einen allgemeinen Graphen dar, in dem grundsätzlich beliebige Beziehungen abgebildet werden können.
Fehlende Normalisierung
Ein Fakt, der scheinbar oft nicht realisiert wird, ist die fehlende Normalisierung des Modells. Das ändert sich auch dadurch nicht, wenn IDs als Schlüssel eingeführt werden. So findet sich beispielsweise im MySQL-Tutorial das folgende Beispiel.
|
1 2 3 4 5 6 7 8 |
CREATE TABLE category ( id INT UNSIGNED NOT NULL AUTO_INCREMENT, title VARCHAR(255) NOT NULL, parent_id INT UNSIGNED DEFAULT NULL, PRIMARY KEY (id), FOREIGN KEY (parent_id) REFERENCES category (id) ON DELETE CASCADE ON UPDATE CASCADE ); |
Ein Vorgesetzter oder eine übergeordnete Kategorie sind keine Attribute eines Mitarbeiters beziehungsweise einer Kategorie. Mitarbeiter und Vorgesetzte stehen in einem Über-/Unterordnungsverhältnis zueinander in Beziehung. Gleiches gilt für das zitierte Beispiel der Kategorien.
Mitarbeiterinformationen und Beziehungen zwischen den handelnden Personen werden vermischt, um beim Eingangsbeispiel, der Mitarbeiterhierarchie, zu bleiben. Beide Informationen werden gemeinsam in einem Datensatz gespeichert.
In einem Punkt ist das MySQL-Beispiel aber schon besser als das Modell in Listing 1. Das MySQL-Beispiel verwendet numerische Schlüssel statt der Kategoriebezeichner als Verweise. So bleibt einem wenigstens die UPDATE-Anomalie des zuerst gezeigten Modells erspart.
Weiter möchte ich an dieser Stelle gar nicht auf die Normalisierung und mögliche Anomalien eingehen, die daraus resultieren, ein nicht normalisiertes Datenbankmodell zu verwenden. Vielmehr möchte ich auf die strukturelle Integrität und mögliche Anomalien, diese betreffend, zu sprechen kommen.
Strukturelle Anomalien
Bäume und Hierarchien, wie wir sie hier betrachten, stellen eine besondere Form von Graphen dar. Zum einen handelt es sich dabei um einen Baum. Zum anderen, und das differenziert die Hierarchie vom gemeinen Baum, drücken die Beziehungen in einer Hierarchie jeweils ein Über-/Unterordnungsverhältnis aus. Sie haben also eine ganze spezielle semantische Bedeutung. Eine Hierarchie ist also auch ein gerichteter Graph, bei welchem wir die Beziehungen als „hat Vorgesetzten“ oder „hat Mitarbeiter“ lesen können, je nach Blickwinkel. Ansonsten ist einer Hierarchie ein ganz normaler Baum.
Ein Baum ist entweder leer oder besteht aus einem Knoten, dem null oder mehrere Bäume zugeordnet sind.
Aus dieser Definition lassen sich Regeln, die für Bäume und Hierarchien gelten, ableiten:
- Eine Hierarchie ist ein Baum.
- Ist der Baum nicht leer, besitzt er genau einen Wurzelknoten.
- Jeder Knoten im Baum besitzt genau einen übergeordneten Knoten. Hiervon Ausgenommen ist der Wurzelknoten, der keinen Vorgänger übergeordneten Knoten hat.
Weitere Implikationen hieraus sind:
- Mit Ausnahme des Wurzelknotens haben alle Knoten im Baum den Eingangsgrad 1. Der Wurzelknoten hat den Eingangsgrad 0.
- Ein Baum ist zyklenfrei.
Für die praktische Implementierung einer Prsonalhierarchie, die wir hier als Beispiel betrachten, können wir umgangssprachlich das Folgende aus den Regeln sowie den üblichen Integritätsanforderungen formulieren:
- In einer Adjazenztabelle dürfen nur Mitarbeiter referenziert werden, die bereits in einer Personaltabelle erfasst sind.
- Die Vorgesetztenverweise dürfen nur auf Mitarbeiter in der Adjazenztabelle verweisen, die darin bereits als Mitarbeiter erfasst sind. Ausnahme: Wurzelknoten (Chef).
- Mitarbeiter können/dürfen sich nicht selbst als Vorgesetzten referenzieren.
- Die Anzahl der Mitarbeiter (Knoten) ist um 1 größer als die Anzahl der Vorgesetzten (Kanten).
- Die Mitarbeiter-Vorgesetzten-Verweise dürfen keinen Zyklus etablieren.
Allein die Normalisierung verlangt, die Daten in zwei Tabellen aufzuteilen, personal und organisation:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
CREATE TABLE personal ( mnr SERIAL NOT NULL PRIMARY KEY, mitarbeiter VARCHAR(20) NOT NULL, geburtsdatum DATE NOT NULL -- weitere Mitarbeiterattribute ); CREATE TABLE organisation -- Version 2 ( mnr INT NOT NULL PRIMARY KEY, vnr INT, CONSTRAINT fk_organisationoPersonal_mnr FOREIGN KEY (mnr) REFERENCES personal (mnr) ON UPDATE CASCADE, CONSTRAINT fk_organisation2organisation_vnr FOREIGN KEY (vnr) REFERENCES organisation (mnr) ON UPDATE CASCADE ); |
Auf eine DELETE-Kaskade wurde bewusst verzichtet. Sie ist potentiell gefährlich. Mit nur einem einzigen DELETE-Statement könnte der Inhalt der gesamten Hierarchie gelöscht werden.
Hinweis: Bei beispielsweise MySQL funktioniert die UPDATE-Kaskade nicht, obgleich sie syntaktisch akzeptiert wird. Das ist jedoch kein Fehler. Potentiell vorhandene Zyklen, wie sie bei sich selbst referenzierenden Tabellen auftreten können, könnten eine Quasi-Endlosschleife von UPDATE-Operationen auslösen. Das woll(t)en die MySQL-Entwickler vermeiden. Eine DELETE-Kaskade funktioniert aber auch in MySQL. Das hier verwendete PostgreSQL akzeptiert und kann beides..
Mittels dieser einfachen Maßnahmen, Normalisierung, die Wahl geigneter Primäschlüssel und Fremdschlüsselbeziehungen, haben wir das Folgende bereits erreicht:
- Das Datenmodell ist normalisiert.
- Die referentielle Integrität zwischen Personal und den Mitarbeitern in der Organisationshierarchie ist gewährleistet.
- Die referentielle Integrität zwischen Vorgesetzten und Mitarbeitern ist sichergestellt.
- Jeder Mitarbeiter kann nur einen Vorgesetzten haben.
Die strukturelle Integrität der abzubildenden Hierarchie ist noch nicht gewährleistet. Noch ist es möglich, einem Mitarbeiter sich selbst als Vorgesetzten zuzuweisen. Das stellt einen Zirkelschluss dar. Weitere Zirkelschlüsse sind ebenso möglich. So könnte bei einer UPDATE-Operation, Rainer zum Vorgesetzten von Lisa erklärt werden. Die ist jedoch über Silke bereits auch Rainer vorgesetzt, so dass hier ein Zirkelschluss vorläge.
Bei INSERT- und/oder DELETE-Operationen kann ein solcher Zirkelschluss nicht eintreten. Delete-Operationen sind diesbezüglich immer unkritisch. Da bei einer INSERT-Operation vorausgesetzt ist, dass die als Vorgesetzter zu benennende Person bereits vorhanden ist, kann ein bereits vorhandener Mitarbeiter nicht auf die noch einzufügende Person verweisen. Ein Zirkelschluss kann daher, mit den implementierten Regeln, ausschließlich durch UPDATE-Operationen bewirkt werden.
Neben möglichen Zirkelschlüssen sichert die aktuelle Implementierung auch nicht zu, genau eine Wurzel zu haben, wenn die Zuordnungstabelle nicht leer ist. Enthält die Hierarchie keinen Datensatz, so gibt es keinen Wurzelknoten. Der erste Datensatz, welcher eingefügt wird, muss zwingend der Wurzelknoten sein. Andernfalls verstießen wir gegen die referentielle Integrität beim Einfügen weiterer Datensätze. Von diesen darf jedoch kein Datensatz einen NULL-Wert im Vorgesetztenattribut besitzen. Dieser spezielle Wert kennzeichnet in unserer Implementierung die Wurzel, von der es, wenn Datensätze in der Hierarchie gespeichert sind, nur genau eine geben darf.
Hierarchische Strukturen mit Adjazenzlisten optimiert
Schutz vor Selbstbezügen
Am einfachsten auszuschließen ist ein Selbstbezug. Dazu reicht es, eine CHECK-Klausel zu definieren, die auf Spaltenebene prüft, ob die Nummer eines Mitarbeiters der eines Vorgesetzten entspricht. Wenn ja, handelt es sich um einen Verstoß gegen die oben formulierten Regeln.
|
1 2 3 4 5 6 7 8 9 |
CREATE TABLE organisation -- Version 3 ( mnr INT NOT NULL PRIMARY KEY, vnr INT CHECK (mnr <> vnr), CONSTRAINT fk_organisation2personal_mnr FOREIGN KEY (mnr) REFERENCES personal (mnr) ON UPDATE CASCADE, CONSTRAINT fk_organisation2organisation_vnr FOREIGN KEY (vnr) REFERENCES organisation (mnr) ON UPDATE CASCADE ); |
Größere Zyklen, also Zirkelbezüge über mehrere Hierarchieebenen, werden hierdurch nicht ausgeschlossen. Wir behandeln sie im übernächsten Abschnitt.
Zusicherung der Wurzeleigenschaft
Es gibt keine Wurzel, wenn die Hierachie keinen Datensatz beinhaltet. Und es gibt genau eine Wurzel, wenn mindestens ein Datensatz in der Hierachie gespeichert ist. Dies zu gewährleisten ist einfach. Wir haben oben die Regel abgeleitet, dass die Anzahl der Mitarbeiter immer um 1 größer ist als die Anzahl der Vorgesetzten, wenn mindestens ein Datensatz in der Hierarchie gespeichert ist. Eine CHECK-Klausel, die auf Tabellenebene definiert wird, kann/könnte dies leicht prüfen. – Wir werden gleich noch sehen, ob solche eine Regel, auch wenn sie naheliegend ist, eine gute Idee ist.
Hinweis: Je nach Datenbankmanagementsystem können Select-Statements und/oder der Aufruf von Funktionen in einer CHECK-Klausel erlaubt sein oder eben auch nicht. Das hier verwendete Datenbankmanagementsystem, PostgreSQL 13.4, erlaubt den Aufruf von Funktionen. Unterstützt ein Datenbankmanagementsystem weder SQL-Statements noch Funktionen in CHECK-Klauseln, so können im Ergebnis gleiche Regeln mithilfe von berechneten Spalten sowie Triggern erzielt werden.
Um die notwendigen Funktionen zur Bestimmung der Anzahlen von Mitarbeitern und Vorgesetzten bestimmen zu können, muss bereits eine Tabelle organisation existieren. Umgekehrt müssen die genannten Funktionen implementiert sein, um sie in der Tabelledefinition verwenden zu können. Das Vorgehen ist daher so, zuerst die Tabelle zu erzeugen, die Funktionen zu erstellen und danach die erforderliche CHECK-Klausel, welche die neuen Funktionen nutzt, via ALTER TABLE in die Tabelle zu integrieren.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
-- Mitarbeiteranzahl bestimmen CREATE FUNCTION anzahl_mitarbeiter() RETURNS INT AS $$ DECLARE anzahl INT := 0; BEGIN SELECT COUNT(*) INTO anzahl FROM organisation; RETURN anzahl; END; $$ LANGUAGE plpgsql; -- Vorgesetztenanzahl bestimmen CREATE FUNCTION anzahl_vorgesetzte() RETURNS INT AS $$ DECLARE anzahl INT := 0; BEGIN SELECT COUNT(vnr) INTO anzahl FROM organisation; RETURN anzahl; END; $$ LANGUAGE plpgsql; |
Mit dem Vorhandensein der beiden opbigen Funktionen, können wir nun eine Regel formulieren, welche uns die erforderliche Wurzeleigenschaft zusichert.
|
1 2 3 |
ALTER TABLE organisation ADD CONSTRAINT wurzelcheck CHECK (anzahl_mitarbeiter() = anzahl_vorgesetzte() + CASE WHEN vnr IS NULL THEN 0 ELSE 1 END); |
Diese Regel erfüllt ihren Zweck. Leider verhindert Sie aber auch, die Mitarbeiternummer der Wurzel aktualisieren zu können. Die Regel greift, unabhängig von der auszuführenden Aktion. Ist bereits eine Wurzel vorhanden, und soll deren Mitarbeiternummer geändert werden, feuert der erste Teil von CASE, was zu einem Fehler führt. – Eine einmal festgelegt Wurzel nicht ändern zu können, halt ich für eine zu starke Einschränkung.
Statt einer Tabellenregel verwenden wir daher Trigger. Mit ihrer Hilfe können wir die Fälle des Einfügens und des Änderns von Daten einfach unterscheiden. Das ist notwendig, um die oben genannte Regel situativ angepasst anwenden zu können.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
CREATE FUNCTION before_insert_organisationtrigger() RETURNS TRIGGER AS $$ BEGIN IF NOT ((anzahl_mitarbeiter() = anzahl_vorgesetzte() + CASE WHEN NEW.vnr IS NULL THEN 0 ELSE 1 END)) THEN RAISE EXCEPTION 'Wurzeleigenschaft verletzt.'; END IF; RETURN NEW; END; $$ LANGUAGE plpgsql; CREATE TRIGGER before_organisation_insert BEFORE INSERT ON organisation FOR EACH ROW EXECUTE PROCEDURE before_insert_organisationtrigger(); CREATE FUNCTION after_update_organisationtrigger() RETURNS TRIGGER AS $$ BEGIN IF NOT (anzahl_mitarbeiter() = anzahl_vorgesetzte() + 1) THEN RAISE EXCEPTION 'Wurzeleigenschaft verletzt.'; END IF; RETURN NEW; END; $$ LANGUAGE plpgsql; CREATE TRIGGER after_organisation_update AFTER UPDATE ON organisation FOR EACH ROW EXECUTE PROCEDURE after_update_organisationtrigger(); |
Für den INSERT-Trigger gilt: Ist noch kein Datensatz erfasst, ist als erster Datensatz der Wurzelknoten zu setzen. Das sichern bereits die definierten Regeln zur referentiellen Integrität ab. Um nun aber eine Wurzel einfügen zu können, muss dennoch die Anzahl der Mitarbeiter gleich der Anzahl der Vorgesetzen sein. Daher wird im Falle von vnr IS NULL nichts auf die Vorgesetztenanzahl addiert. Da sowohl Mitarbeiter- als auch Vorgesetztenanzahl bei einer leeren Tabelle 0 sind, ist die Welt in Ordnung. Würde versucht, einen „normalen“ Mitarbeiter einzufügen, würde 1 auf die Vorgesetztenanzahl addiert, was dann zu einem Fehler führen würde. Dadurch wird sichergestellt, als ersten Datensatz den Wurzelknoten zu setzen. Bei später einzufügenden Datensätzen verhält es sich dann analog.
UPDATE-Operationen können nur ausgeführt werden, wenn Datensätze vorhanden sind. Die Anzahl der Mitarbeiter muss also immer den Anzahl der Vorgesetzten plus eins sein. Bei einem UPDATE-Trigger muss diese Bedingung nach der Operation überprüft werden, weil ein Update einen inkonsistenten Zustand erzeugen könnte.
Die Wurzel kann aufgrund der etablierten Fremdschlüsselbeziehungen auch nicht gelöscht werden, sodass die Wurzeleigenschaften eines Hierarchie, eines Baumes ganz allgemein, gewährleistet sind.
Zyklen
Die bereits getroffene Maßnahme, Selbstbezüge zu verhindern, reicht nicht aus, einen Zyklus über mehrere Ebenen zu unterbinden. Ein Zyklus kann, dank der bereits implementierten Regeln, nicht beim Einfügen oder Löschen von Datensätzen etabliert werden. Lediglich UPDATE-Operationen können einen Zirkelschluss zwischen vorhandenen Datensätzen bewirken.
Wenn die folgenden Daten in die Hierarchie eingefügt seien, dann bewirkt ein UPDATE-Statement, wie das in Zeile 12, einen Zirkelschluss. Damit einhergehend würde auch die Gesamtstruktur der Hierarchie zerstört, ohne die bisher implementierten Regeln zu verletzen.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
INSERT INTO personal(mitarbeiter, geburtsdatum) VALUES ('Wolfgang', '1980-12-06') /*1*/ , ('Sebastian', '1979-10-03') /*2*/ , ('Mario', '2002-09-03') /*3*/ , ('Lisa', '1980-12-01') /*4*/ , ('Silke', '1985-01-06') /*5*/ , ('Bernd', '1989-11-27') /*6*/ , ('Rainer', '1995-12-01') /*7*/ , ('Robert', '1984-07-16') /*8*/ , ('Marius', '1989-02-05') /*9*/; INSERT INTO organisation (mnr, vnr) VALUES (1, NULL), (2, 1), (3, 2), (4, 1), (5, 4) , (6, 5), (7, 5), (8, 4), (9, 4); UPDATE organisation SET vnr = 7 WHERE mnr = 4; |
Zur Vermeidung von Zirkelschlüssen brauchen wir einen weiteren UPDATE-Trigger. Die Idee, die diesem Trigger zugrundeliegt, ist im Prinzip einfach. Wir analysieren den Teilbaum, zu welchem der zu ändernde Datensatz die Wurzel darstellt. Kommt die neu zu setzende Vorgesetztennummer im Teilbaum als Mitarbeiternummer vor, würde eine solche Datensatzaktualsierung einen Zirkelschluss bewirken.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
CREATE FUNCTION before_update_organisationtrigger() RETURNS TRIGGER AS $$ DECLARE anzahl INT := 0; BEGIN SELECT COUNT(mnr) INTO anzahl FROM ( WITH RECURSIVE teilbaum (mnr, vnr) AS ( SELECT o1.mnr, o1.vnr FROM organisation o1 WHERE o1.vnr = old.mnr UNION SELECT o2.mnr, o2.vnr FROM organisation o2 JOIN teilbaum AS tb ON tb.mnr = o2.vnr ) SELECT mnr FROM teilbaum ) hlp WHERE mnr = new.vnr; IF (anzahl > 0) THEN RAISE EXCEPTION 'Zirkelschluss registriert.'; END IF; RETURN NEW; END; $$ LANGUAGE plpgsql; CREATE TRIGGER before_organisation_update BEFORE UPDATE ON organisation FOR EACH ROW EXECUTE PROCEDURE before_update_organisationtrigger(); |
Ein UPDATE-Statement, welches einen Zirkelschluss erzeugen würde, ist nunmehr nicht ausführbar. Die Hierarchie ist damit fertig implementiert. Sie ist normalisiert und Regeln für die referentielle und strukturelle Integrität wurden etabliert.
Zu guter letzt spendieren wir uns aber doch noch einen Index, um Vorgesetzte schneller finden zu können. Bei der Anzahl der Beispielhaften ein absolutes MUST HAVE (* GRINS *)
|
1 |
CREATE INDEX idx_organisation_vnr ON organisation (vnr); |
Navigation und Operationen im hierarchischen Adjazenzlistenmodell
Die wohl einfachste Aufgabe besteht darin, die Wurzel einer Hierarchie zu finden. Die hier implementierte Hierarchie zeichnet sich dadurch aus, dass die Wurzel keinen Vorfahren hat, das entsprechende Attribut daher mit NULL besetzt ist. Es gibt abweichende Modellierungen, was dann natürlich auch Auswirkungen auf die zu implementierenden Regeln und Abfragen hat. Wir nutzen das hier implementierte Datenmodell.
Finden der Wurzel
|
1 2 3 |
SELECT * FROM organisation WHERE vnr IS NULL; -- das kennzeichnet die Wurzel |
Wollen wir auch den Namen des Chefs in Erfahrung bringen, bilden wir einen Join mit der Personaltabelle.
|
1 2 3 4 |
SELECT o.mnr, p.mitarbeiter FROM organisation AS o JOIN personal AS p ON o.mnr = p.mnr WHERE vnr IS NULL; |
Finden von Blättern
Blätter in einem Baum sind diejenigen Knoten, die keinen Nachfolger haben. Das bedeutet, diejenigen Knoten finden zu müssen, die nicht in der Menge der Mitarbeiter sind, deren Mitarbeiternummer als Vorgesetztennummer auftritt. Diese Aufgabe können wir mit einer korrelierten Unterabfrage lösen.
|
1 2 3 4 5 6 7 |
SELECT o1.mnr FROM organisation AS o1 WHERE NOT EXISTS( SELECT * FROM organisation AS o2 WHERE o1.mnr = o2.vnr ); |
Ebenen ausgeben
Die klassische Abfragemethode, nutzt Self-Joins, um eine Hierarchie ebenenweise auszugeben.
|
1 2 3 4 5 |
SELECT o1.mnr AS e0, o2.mnr AS e1 FROM Organisation AS o1 LEFT JOIN Organisation AS o2 ON o1.mnr = o2.vnr WHERE o1.mnr = 1 ORDER BY e0, e1; |
Eine weitere Ebene in die Ausgabe aufzunehmen, bedeutet einen weiteren Self-Join. Dieses Prinzip ist für jede weitere Ebene, die ausgegeben werden soll, zu wiederholen. Weil die Anzahl der Ebenen nicht unbedingt im Vornherein bekannt ist, stellt sich die Frage, wieviele Joins erforderlich sind, die gesamte Hierarchie auszugeben.
|
1 2 3 4 5 6 7 |
SELECT o1.mnr AS e0, o2.mnr AS e1, o3.mnr AS e2, o4.mnr AS e3 FROM Organisation AS o1 LEFT JOIN Organisation AS o2 ON o1.mnr = o2.vnr LEFT JOIN Organisation AS o3 ON o2.mnr = o3.vnr LEFT JOIN Organisation AS o4 ON o3.mnr = o4.vnr WHERE o1.mnr = 1 ORDER BY e0, e1, e2, e3; |
Moderne Datenbankmanagementsysteme unterstützen rekursive CTE (Common Table Expression). Damit lassen sich rekursive Datenstrukturen, wie die von Bäumen, einfach traversieren.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
WITH RECURSIVE orgstruktur (mnr, vnr, ebene) AS ( -- die Rekursion startet mit der Ankerabfrage SELECT o1.mnr, o1.vnr, 0 as ebene FROM organisation AS o1 WHERE vnr IS NULL -- Wurzel als Anker UNION ALL -- Rekursionsabfrage SELECT o2.mnr, o2.vnr, ebene+1 FROM organisation AS o2 JOIN orgstruktur AS ot ON ot.mnr = o2.vnr ) SELECT ot.vnr AS vnr, p2.mitarbeiter AS vorgesetzter , ot.mnr AS mnr, p1.mitarbeiter AS mitarbeiter, ebene FROM orgstruktur AS ot JOIN personal AS p1 ON ot.mnr = p1.mnr LEFT JOIN personal AS p2 ON ot.vnr = p2.mnr; |
Die erste Abfrage eines rekursiven CTE ist die so genannte Ankerabfrage. Die mit UNION oder UNION ALL verknüpfte Abfrage ist die Rekursionsabfrage, die den CTE selbst referenziert.
Der Left-Join ist erforderlich, weil der Vorgesetztenverweis der Wurzel (Wolfang) NULL ist.
Teilbaum ausgeben
Gelegentlich sind wir nur an einem Teilbaum der Hierarchie interessiert.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
WITH RECURSIVE orgstruktur (mnr, vnr) AS ( -- die Rekursion startet mit der Ankerabfrage SELECT o1.mnr, o1.vnr FROM organisation AS o1 WHERE mnr = 4 -- Lisa als Anker UNION ALL -- Rekursionsabfrage SELECT o2.mnr, o2.vnr FROM organisation AS o2 JOIN orgstruktur AS ot ON ot.mnr = o2.vnr ) SELECT mnr FROM orgstruktur; |
Wollen wir lediglich wissen, welche Mitarbeiter einem bestimmten Mitarbeiter unterstellt sind, so erreichen wir das durch eine kleine Änderung in der Ankerabfrage. Wir haben dies bereits im UPDATE-Trigger, Listing 9, genutzt.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
WITH RECURSIVE orgstruktur (mnr, vnr) AS ( -- die Rekursion startet mit der Ankerabfrage SELECT o1.mnr, o1.vnr FROM organisation AS o1 WHERE vnr = 4 -- Lisa als Anker, aber OHNE Lisa selbst UNION ALL -- Rekursionsabfrage SELECT o2.mnr, o2.vnr FROM organisation AS o2 JOIN orgstruktur AS ot ON ot.mnr = o2.vnr ) SELECT ot.mnr AS mnr, p1.mitarbeiter AS mitarbeiter FROM orgstruktur AS ot JOIN personal AS p1 ON ot.mnr = p1.mnr; |
Knoten und/oder Teilbaum löschen
Das Löschen eines Blattes ist trivial. Wir brauchen das nicht zu besprechen. Hängen von einem Knoten jedoch weitere Knoten ab, dann kommt es darauf an, ob die Tabelle eine DELETE-Kaskade definiert hat oder nicht. Ist eine solche definiert, wird mit Löschen eines Knotens der gesamte Teilbaum, der von ihm abhängig ist, gelöscht. Mit dem Löschen des Wurzelknotens wird dann der ganze Baum gelöscht. Im vorliegenden Beispiel haben wir daher auf eine DELETE-Kaskade verzichtet.
Soll ein Teilbaum gelöscht werden, so haben wir dessen Knoten zu ermitteln. Das Resultat verwenden wir im DELETE-Statement, um die zu löschenden Knoten zu benennen.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
WITH RECURSIVE orgstruktur (mnr, vnr) AS ( -- die Rekursion startet mit der Ankerabfrage SELECT o1.mnr, o1.vnr FROM organisation AS o1 WHERE mnr = 4 -- Teilbaum inklusive Lisa löschen UNION ALL -- vnr, um nur ihre Mitarbeiter zu löschen -- Rekursionsabfrage SELECT o2.mnr, o2.vnr FROM organisation AS o2 JOIN orgstruktur AS ot ON ot.mnr = o2.vnr ) DELETE FROM organisation WHERE mnr IN ( SELECT mnr FROM orgstruktur ); |
Das Statement lässt sich deshalb so einfach formulieren, ohne die Reihenfolge der zu löschenden Knoten zu beachten, weil gemäß SQL-Standard die Integritätsbedingungen aufgeschoben geprüft werden. Datenbankmanagementsysteme, die sich nicht an den Standard halten, und eine Prüfung nach jedem einzelnen Datensatz, der gelöscht wird, vornehmen, müssen dagegen die Reihenfolge beachten.
Als Beispiel sei hier gezeigt, wie das in MySQL zu bewirken ist, wenn, so wie hier, keine ON DELETE CASCADE-Klausel definiert wurde. Die würde mit dem Löschen eines Datensatzes gleich alle abhängigen Datensätze mit löschen. Das Problem wäre dann auf einfachste Art und Weise gelöst. Allerdings nimmt man dann in Kauf, auch versehentlich ganz schnell einen Teilbaum zu löschen. Will man das verhindern, so verzichtet man auf das ON DELETE CASCADE. Dann wird das Löschen eines Teilbaums allerdings etwas trickreich, weil wir die zu löschenden Mitarbeiternummern, von den Blättern des Baums aufsteigend, benötigen, um sie löschen zu können.
Der hier angewendete Trick besteht darin, die Mitarbeiternummern in umgekehrter Ebenenreihenfolge mithilfe von group_concat() zu sammeln und in einer Liste, einer Sessionvariablen, zu speichern. Damit die folgende DELETE-Operation nun auch diese Reihenfolge befolgt, müssen wir dem DELETE noch mitteilen, sie in der Reihenfolge ihres Auftretens in der Liste zu löschen.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
SELECT group_concat(mnr ORDER BY ebene DESC) INTO @mnrlist FROM ( WITH RECURSIVE orgstruktur (mnr, vnr, ebene) AS ( SELECT o1.mnr, o1.vnr, 0 as ebene FROM organisation AS o1 WHERE mnr = 4 -- Teilbaum von Lisa löschen UNION ALL SELECT o2.mnr, o2.vnr, ebene+1 FROM organisation AS o2 JOIN orgstruktur AS ot ON ot.mnr = o2.vnr ) SELECT mnr, ebene from orgstruktur ) hlp; DELETE FROM organisation WHERE find_in_set(mnr, @mnrlist) ORDER BY find_in_set(mnr, @mnrlist); |
Weil die Statements zum Löschen eines Teilbaumes grundsätzlich etwas länglich sind, bietet es sich in der Praxis an, sie in eine Stored Procedure zu hüllen.
Teilbaum verschieben
Das Verschieben eines Knotens (inklusive seines eventuell vorhandenen Unterbaums) ist trivial. Man ändert einfach desssen Vorgesetztenverweis. Komplexer wird es jedoch, wenn zwei Knoten vertauscht werden sollen.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
CREATE PROCEDURE swap_mitarbeiter(m1 INT, m2 INT) AS $$ DECLARE dummy INT := 0; BEGIN IF (m1 <> m2) THEN -- es gibt nur etwas zu tun, wenn m1, m2 verschieden INSERT INTO personal (mnr, mitarbeiter, geburtsdatum) VALUES (0, '{{ DUMMY }}', '1900-01-01'); -- Dummy-Mitarbeiter anlegen UPDATE organisation SET mnr = dummy WHERE mnr = m1; UPDATE organisation SET mnr = m1 WHERE mnr = m2; UPDATE organisation SET mnr = m2 WHERE mnr = dummy; DELETE FROM personal WHERE mnr = dummy; -- lösche Dummy-Mitarbeiter END IF; END; $$ LANGUAGE plpgsql; |
Weil das Prozedere mehrere Schritte erfordert, die zudem in der korrekten Reihenfolge auszuführen sind, bietet es sich an, dafür eine Prozedur zu schreiben. Wir brauchen außerdem einen temporären Dummy als Hilfsvariable, weil sich zwei Werte nicht direkt tauschen lassen. Nach Gebrauch, kann der Dummy wieder gelöscht werden.
Einfügen von Knoten
INSERT- und UPDATE-Operationen sind trivial. Diese Operationen bedürfen im Adjazenzlistenmodell keiner weiteren Behandlung.
|
1 2 3 4 |
INSERT INTO personal (mitarbeiter, geburtsdatum) VALUES ('Donald', '1900-01-01'); INSERT INTO organisation(mnr, vnr) VALUES (10, 1); |
Die notwendigen Regeln, die zur Einhaltung der referentiellen und strukturellen Integrität einzuhalten sind, haben wir implementiert.
Pfade und Pfadlängen
Ein Weg zwischen zwei Knoten wird als Pfad bezeichnet, wenn der Weg keine doppelten Knoten aufweist. Üblicherweise interessieren wir uns in einer Hierarchie für die Pfade und deren Längen, die Anzahl der Kanten, zwischen zwei Knoten, die in einem Über-/Unterordnungsverhältnis zueinander stehen.
Der Pfad von Lisa zu Rainer hat beispielsweise die Länge 2 und geht über Silke.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
WITH RECURSIVE pfade (vnr, mnr, laenge, pfad) AS ( SELECT vnr, mnr, 1 AS laenge, concat(vnr, ', ', mnr) as pfad FROM organisation WHERE vnr = 4 -- Lisa UNION ALL SELECT pfade.vnr, organisation.mnr, pfade.laenge+1, concat(pfade.pfad, ', ', organisation.mnr) FROM organisation JOIN pfade ON organisation.vnr = pfade.mnr ) SELECT vnr, mnr, laenge, pfad FROM pfade WHERE vnr = 4 and mnr = 7; -- Zwischenwerte ausfiltern |
Das Statement untersucht die Hierarchie von oben nach unten. Das ist insoweit ineffzient, als alle Pfade beschritten werden, die vom Mitarbeiter der Ankerabfrage ausgehen. Bottom-Up wird dies vermieden.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
WITH RECURSIVE pfade (vnr, mnr, laenge, pfad) AS ( SELECT vnr, mnr, 1 AS laenge, concat(vnr, ', ', mnr) AS pfad FROM organisation WHERE mnr = 7 -- Rainer UNION ALL SELECT organisation.vnr, pfade.mnr, pfade.laenge+1, concat(organisation.vnr, ', ', pfade.pfad) FROM organisation JOIN pfade ON organisation.mnr = pfade.vnr AND organisation.mnr <> 4 -- Lisa ) SELECT * FROM pfade WHERE vnr = 4 AND mnr = 7; -- Zwischenwerte ausfiltern |
Zwischenfazit
Bevor wir uns in den kommenden zwei Beiträgen mit alternativen Implementierungen hierarchischer Strukturen befassen, wollen wir ein kurzes Zwischenfazit ziehen.
Je nach Datenbankmanagementsystem, ist es mehr oder minder unkritisch, die notwendigen Regeln zu implementieren, welche uns die referentielle und strukturelle Integrität unserer Daten gewährleisten. Hierarchische Strukturen mit Adjazenzlisten abzubilden ist ein relativ einfach zu beschreitender Weg. Wir sollten jedoch nicht vergessen, das Rekursionsabfragen immer auch viel Rechenleistung benötigen. Bäume werden oftmals, so auch in diesem Beitrag, rekursiv definiert. Rekursive Strukturen und Algorithmen zu verwenden, um sie zu handhaben, ist daher naheliegend. Wer viele Einfüge-, Lösch- und Änderungsoperationen an einer hierarchischen Datenstruktur vorzunehmen hat, der ist mit einer Adjazenzlistenimplementierung sicher gut beraten. Geht es jedoch vorwiegend um Abfragegeschwindigkeit, so werden wir an dieser Stelle noch alternative Implementierungen vorstellen und diskutieren.